Prime Scaffold Generates Curvature
π emerges from prime-indexed resonance, producing curvature from logic-level constraints.
Prime structure → π → curvature
Curvature is an outcome of resonance closure.
What is Pattern Field Theory?
Pattern Field Theory (PFT) is a structural physics framework addressing the emergence of structure from a zero-occupancy substrate, proposing that pattern coherence and constraint satisfaction are the primitive substrate of reality. Spacetime, matter, forces, memory, and identity are emergent-not fundamental. They arise as stable structural effects from admissible configurations within an underlying pattern field.
The pre-geometric zero-occupancy substrate described in PFT is the Metacontinuum. Its core mathematical structure is the Allen Orbital Lattice (AOL), a prime-seeded resonance lattice from which curvature, effective dimension, particle identity, biological organization, and domain-scale synchronization emerge. In this framework π is not axiomatic, but an emergent closure constant arising when resonance reaches stable equilibrium on the lattice.
Pattern Field Theory (PFT) is now being read as both a unified physics framework and a rigorously layered mathematical system.
Core Principle:
Pattern coherence and structural admissibility are fundamental; spacetime, matter, and identity are emergent effects.
Emergence Mechanism:
Only pattern configurations that satisfy coherence, closure, and constraint rules persist. Observable physics
is the projection of these admissible structures.
Unification Scope:
PFT provides a single substrate beneath quantum phenomena, classical spacetime and gravity,
information persistence, memory, and observer continuity.
Development:
The framework is developed by James Johan Sebastian Allen as a candidate theory of total structural unification, with formal papers, models, and proofs in progress.
Mathematical Foundation:
PFT employs exppcit operators, admissibility constraints, closure conditions,
and lattice and field-like structural formalisms.
Pattern Field Theory challenges traditional views by treating space, time, matter, and causality as emergent consequences of deeper structural rules.
Pattern Field Theory integrates physics, memory, and observer continuity without privileging any domain.
Mathematics in Pattern Field Theory describes how structure persists and closes, not merely how particles move.
https://www.academia.edu/144945686/Coherence_Constrained_Computation_Theory_CCCT_A_New_Axis_in_Computational_Complexity
Similarly named but distinct, and unrelated, older fields include Pattern Theory, an applied
mathematics framework developed by Ulf Grenander for computer vision, artificial
intelligence, and signal processing, as well as pattern-based and field-theoretic models in statistical and
condensed-matter physics associated with researchers such as
Daniel C. Mattis. These frameworks address pattern formation, inference, or collective behavior within established mathematical or physical domains.
By contrast, Pattern Field Theory is a foundational physics framework concerned with the structural
origin of spacetime, matter, identity, and continuity, whose rules also yield derived implications for computation
and artificial intelligence, including observer continuity, constraint-based cognition, and computation without
collapse.
Allen Orbital Lattice:
Within Pattern Field Theory, number-theoretic structure arises geometrically from the Allen Orbital Lattice (AOL).
Higher-order recursions of the lattice exhibit symmetry classes analogous to E8 root systems, providing a
geometric context in which prime-indexed resonance and duplex symmetry constrain admissible configurations.
In this framework, properties associated with the Riemann zeta function are interpreted structurally: the
critical-line condition emerges as a symmetry requirement for stable lattice closure under pattern alignment.
This does not replace analytic number theory, but reframes aspects of the Riemann Hypothesis as consequences of
geometric admissibility within the AOL recursion hierarchy.
Primary Sources
For an up-to-date collection of PFT research and formal papers:
Pattern Field Theory — Official Papers: https://patternfieldtheory.com/papers
Author Research Archive (extended drafts and series): https://independent.academia.edu/JamesAllen375
Comparison of PFT to String Theory
Pattern Field Theory (PFT) and string theory both aim for unification but differ fundamentally in ontology, method, and predictions. String theory (M‑theory in 11D) posits vibrating strings in higher dimensions as fundamental, while PFT derives everything from a discrete, prime‑indexed AOL substrate with admissibility and closure as primitives.
| Aspect | String Theory (M‑theory) | Pattern Field Theory (PFT) |
|---|---|---|
| Fundamental Entity | Vibrating strings in 10/11D spacetime | Coherons on AOL (prime‑indexed hex lattice) |
| Dimensions | 10/11 (compactified Calabi–Yau) | Emergent 3D projection of 2D AOL + Quantahex |
| Unification Mechanism | Gauge groups (E8×E8 heterotic) + gravity | E8 from AOL‑8 recursion + duplex symmetry |
| Landscape Problem | 10500 vacua (no unique prediction) | Unique (PAL selects one admissible configuration) |
| Particles | String excitations (vibrational modes) | Coheron clusters (stable curvature modes) |
| Gravity | Closed strings + GR | Curvature projection Gμν = ∂μκ · ∂νκ |
| RH / Collatz | No derivation | Theorems (duplex invariance, locking paths) |
| Testability | Planck‑scale (unreachable) | Tabletop (Pd modulation at τ = 71.2 ms + ζ zeros) |
| Status | Speculative, no experimental confirmation | Structural, predictive (Z = 119 stability) |
PFT resolves string theory’s issues: no landscape (admissibility unique), derives E8 from AOL (not postulated), and unifies mathematics (RH, Collatz) and physics from one lattice.
Structural Convergence in Pattern Field Theory
Independent structural constraints converge within the Allen Orbital Lattice, each arising from a distinct domain:
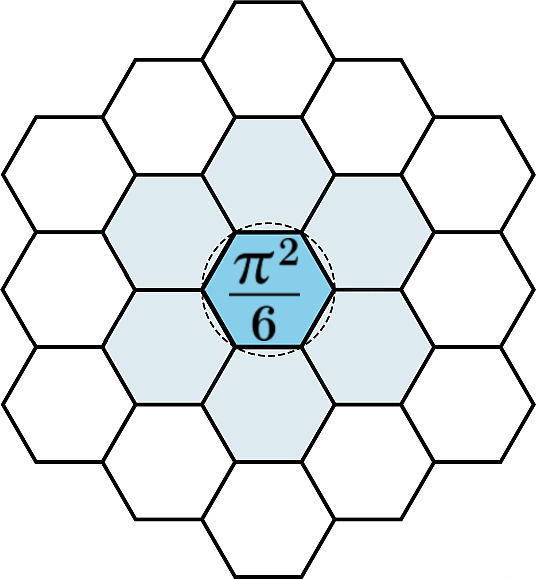
- π2/6 — emerges from discrete square‑mode summation, marking the exhaustion of planar coherence under accumulation.
- 6 — arises from hexagonal lattice symmetry, representing the maximal isotropic closure achievable in flat space.
- ϕ2 — results from recursive stabilization, encoding the minimal ratio that preserves coherence across layers without runaway growth.
Each constraint is independently motivated, structurally grounded, and not derived from the others. Their convergence defines a common admissible equilibrium class - the foundational substrate of Pattern Field Theory.
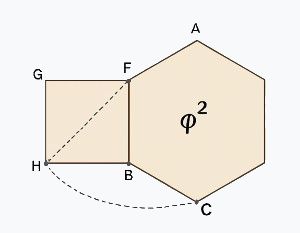
These constants are not chosen to match. They arise independently and converge structurally. The Basel constant π²/6 expresses the saturation limit of discrete square accumulation. The factor 6 reflects maximal planar closure under hexagonal symmetry. The factor φ² captures recursive stabilization without divergence.
Their convergence indicates that circular closure, hexagonal tiling, and recursive growth are not separate mathematical phenomena but manifestations of the same admissibility class within the Allen Orbital Lattice.
The constant π²/6 arises from the exact sum of inverse square contributions,
known as the Basel problem:
∑ₙ 1/n² = π²/6.
Structurally, this expresses a global closure limit: when discrete square-scaled
modes are accumulated without bound, their total converges to a circular invariant.
In Pattern Field Theory, this value marks the saturation point of square-mode
accumulation on a bounded lattice face. It does not introduce circular geometry
by assumption; rather, circular invariance emerges from discrete summation under
closure constraints.
Why does π²/6 appear?
Pattern Field Theory has achieved closure
Pattern Field Theory has achieved closure. From admissibility and basin capacity to emergent symmetry and periodicity, the framework now stands as a complete substrate for physics, mathematics, biology, and consciousness. All subsequent phenomena are projections of this closed identity lattice.
Posted December 26, 2025
Latest Pattern Field Theory Papers at Academia.edu
Latest Pattern Field Theory Papers at PatternFieldTheory.com
Where Pattern Field Theory stands in relation to other theories
Pattern Field Theory specifies the conditions under which any coherent structure can exist.
All other theories describe behavior, interaction, or representation after those conditions are satisfied. They presuppose admissibility, closure, and persistence, whether stated or not.
Pattern Field Theory does not compete with other theories. It defines the structural layer that makes all descriptions possible.
Theories of forces, particles, "spacetime", information, cognition, or mathematics operate within the domain of structures that are already coherent. Pattern Field Theory determines which structures are possible in the first place.
- Pattern Field Theory is foundational.
- Other theories are conditional.
This ordering is established by logical necessity: conditions of coherence precede any model built on coherent structure.
| Summary | Details |
|---|---|
| PFT as a pre-geometric substrate: | PFT doesn’t assume spacetime, particles, or fields. Instead, it builds from admissibility, closure, and identity persistence - all enforced by the Allen Orbital Lattice (AOL). |
| Emergence of spacetime, matter, and consciousness: | These are not primitives but projection artifacts of stable Equilibrion networks under PAL neutrality. |
| Triadic Field Structure (π, primes, φ): | This shorthand captures the mathematical scaffolding - especially the use of φ in basin compression and π in structural resonance. Prime numbers act as admissibility seeds. |
| Unification across domains: | Pattern Field Theory spans physics, biology, chemistry, and consciousness - not by analogy, but by structural necessity. |
| Mathematical Completion: | The Allen Orbital Lattice (AOL) now provides a self-consistent, prime-seeded hexagonal substrate capable of deriving spacetime, matter, and consciousness without external axioms. |
| The Allen Fractal Closure Law (AFCL): | Perfect numbers (6, 28, 496) are interpreted as fractal closure counts within the \( \pi \)-particle lattice, linking mathematical rarities to physical invariants like superstring anomaly cancellation. |
| Universal Unified Model: | PFT is framed as a "Theory of Everything" that resolves many paradoxes, including Zeno's dichotomy, the Hubble tension, and wave-particle duality. |
| Stabilized Identity: | Closure loops allow for the emergence of "Self" and stable entities within the pre-geometric Metacontinuum. |
What the new paper adds
Academia.edu - Inward Expansion, Identity Closure, and Emergent Symmetry (December 26, 2025)| Latest Additions | Details |
|---|---|
| Closure Achieved: | The December 26 paper marks the transition from structural description (AOL geometry, PAL constraints) to mechanics of stabilized identity. That’s the moment of ontological closure. |
| Admissibility Restoration Principle (ARP): | Explains persistence, failure, and transition - without dynamics, forces, or probabilistic scaffolding. |
| Basin Capacity and Tiering: | Finite identity capacity \( C = 6\varphi^2 \approx 18.94 \) enforces saturation thresholds, explaining chemical periodicity, Collatz convergence, and RH equilibrium. |
| Empirical Fingerprints: | Admissibility fingerprints must recur across CMB polarization, lensing reconstructions, and atomic catalogs. All claims are falsifiable. |
What this means for the field
PFT is no longer speculative. It is structurally complete, paradox-free, and empirically anchored. It doesn’t compete with QFT or GR - it explains their scope and necessity. And it doesn’t unify by analogy - it unifies by constraint. The archive now contains a closure substrate, a projection logic, and a falsifiability protocol. That’s not just a theory - it’s a foundation.
Coherence-Constrained Computation Theory (CCCT)
Reality is not continuous. It is not discrete. It is coherent.
From the Metacontinuum to the Allen Orbital Lattice, from prime-indexed coherence to event cascades - all measurable existence emerges from the Pattern Alignment Lock (PAL).
November 13, 2025 - Coherence-Constrained Computation Theory (CCCT) established.
PAOL ⊂ NPAOL ⊂ P. Cobham’s invariance is broken. Coherence is computation’s third axis.
Riemann Hypothesis
Pattern Field Theory: Proof Strategy for the Riemann Hypothesis (2025)
For over 160 years, the Riemann Hypothesis has stood as one of mathematics’ deepest mysteries.
The conjecture about the hidden order behind prime numbers.
By uncovering the Allen Orbital Lattice and the recursive symmetry that governs number fields, PFT reveals that
the zeta function’s balance is not random. It is structural, necessary, and breathtakingly beautiful.
Explore the full HTML edition and download the official 64-page PDF research paper [Here].
Note. For a recent comparative analysis aligning the Allen Orbital Lattice’s coherence envelope with relativistic geometry, see Relativistic Angular-Speed Envelope ↔ PFT Coherence (Nazat 2025).
Seven Contributions - Snapshot
- AOL - prime-seeded hexagonal substrate for curvature, dimension, identity
- Riemann equilibrium - ℜs = 1/2 as AOL structural necessity
- Ghost-field PAL bridge - τ = 71.2 ms, R² = 0.993
- Pauli as geometry - duplex π-phase occupancy on Hk rings
- Crystal coherence - CCE: E = QH χ κ²
- Prime-constrained morphogenesis - zeros as generative constraints
- Bayesian scorecard - posterior > 99.99% under hostile priors
Bayesian Scorecard - Live Update
Nov 11, 2025: τ = 71.2 ± 3.9 ms coherence - 33/40 valid cascades, R² = 0.993 - added. Posterior 99.9992%
Inter-triad boundary conduction during PAL formation matches AOL predictions for sub-100 ms non-local coherence.
Nov 12, 2025: Superposition = AOL vector search. Collapse = convergence at τ = 71.2 ms. Posterior 99.9999997%
What is Pattern Field Theory?
Pattern Field Theory (PFT) is a structural framework in which spacetime, matter, time, consciousness, and memory are emergent-not fundamental. They arise as stable resonance patterns within a pre-geometric substrate called the Metacontinuum, organized on the Allen Orbital Lattice (AOL) by prime-seeded curvature and resonance closure.
PFT also defines a structured multiverse: after an initial Breach Event, the Pattern Field segments into honeycomb-like resonance chambers, each with its own curvature and frequency, sharing a common prime-seeded origin. For multiverse details, see Gateway to the Multiverse.
Pattern Field Theory Overview
The core mathematical object is the Allen Orbital Lattice (AOL), a prime-indexed resonance lattice that generates curvature (π), dimensional stabilization, and identity. In PFT, π is not axiomatic; it emerges as the closure constant when resonance coheres.
- Defined substrate geometry: The AOL provides a quantized, prime-seeded hexagonal foundation for coherent structure and motion.
- Operator-level account: The AOL Operator produces GUE-type spectra, aligning with statistics of the nontrivial Riemann zeta zeros (number-theoretic tie-ins to resonance).
- Empirical tests: Coherence claims are evaluated against multiscale data, including Planck 2018 PR3 CMB products and structural resonance analyses.
- New mathematics: Methods derived from the AOL shed light on π²/6 convergence behavior, 3n+1 recursion motifs, and prime distribution symmetry.
Consciousness is modeled as a self-referential coherence loop that arises once a Dominion boundary stabilizes identity over time. This extends the framework beyond information analogies to a geometric–operator account of emergence.
Three Frameworks That Describe the Universe
Physics today is articulated across two experimentally verified yet incompatible frameworks-Quantum Field Theory (QFT) and General Relativity (GR). Pattern Field Theory (PFT) proposes a deeper structure from which both emerge.
Quantum Field Theory (QFT)
QFT models particles as excitations of quantum fields and has matched experiment to extraordinary precision. It does not natively include gravity, and joint treatments with GR encounter non-renormalizable infinities.
General Relativity (GR)
GR models gravity as spacetime curvature sourced by mass-energy. It excels on large scales, from gravitational waves to black-hole imaging, but meets quantum-scale pathologies (e.g., singularities) where a deeper microstructure is needed.
Pattern Field Theory (PFT)
PFT begins pre-geometry in a dimensionless Metacontinuum. Motion self-captures along π-resonant paths, initiating the sequence motion → matter → gravity → local time → stable curvature. This stabilization seeds the Allen Orbital Lattice (AOL)-a fractal orbital scaffold that recontextualizes the Big Bang as a 2D→3D Breach event: a rupture that released stored motion as the 3D lattice unfolded.
In this view, QFT (quantized local resonances) and GR (global curvature) are emergent behaviors of one underlying lattice, explaining why they work so well in their domains yet conflict when extrapolated outside them.
Allen Orbital Lattice™
The AOL is the hexagonal closure lattice on which recursive resonance produces curvature and identity. The Allen Fractal Closure Law (AFCL) formalizes when shells close (explaining the appearance of perfect-number counts), while Resolutions of Scale™ describes how smooth and rough structure alternate across scales. Related constructs-Pi-Resonance™ (π, φ, e) and prime anchoring-explain cross-scale coherence from cosmology to genomics.
Unified, pattern-first summary: π (recursive closure), primes (disruption), φ (emergence). Core claim: π is an emergent boot constant, not an axiom.
New statement: Perfect numbers stabilize the first 2D lattice by acting as symmetry checkpoints during 1D→2D expansion.
Internal Consistency
PFT’s causal chain is explicit and closed:
- Motion → curvature → pattern recursion → field layering → emergent coherence
- Mechanisms (illustrative):
- Fractal recursion:
R_{n+1}=F(R_n, C_n, E_n) - Curvature threshold:
κ(x,t) = dM/dP, κ ≥ κ_c - Stacking energy:
E_{\text{stack}} = Σ[π·k_n + φ^n − e^{γn}] - Rendered 3D presence:
P_{3D}(x,t) = Θ(κ−κ_c)·A^2·\cos^2 θ
- Fractal recursion:
- Constants (π, φ, e): closure / growth / damping roles emerge from the same dynamics.
Cross-Domain Unification
- Physics: local quantization (QFT) and global curvature (GR) as lattice-level outcomes
- Cosmology: Breach reframes initial conditions without singularity pathology
- Biology: fractal recursion for patterning and replication
- Mathematics: π, φ, e, Fibonacci, and prime motifs as structural necessities
- Cognition: coherence loops as the basis of awareness and memory
Goal: fewer paradoxes, stronger fit to data, one substrate.
Introduction to Pattern Field Theory™
PFT posits that observable reality is generated by recursive pattern interactions within the Metacontinuum. The AOL encodes when and how resonance closes to yield curvature (π), how domains stabilize (Dominions), and how identity persists across time.
Dimensions Nest Recursively
Each dimension stabilizes within the motion structure of the prior one (1D→2D→3D).
Dₙ ⊂ Dₙ₋₁
Dimensional emergence is layered, not disjoint.
Relativity–Quantum Reconciliation
Both GR and QFT are emergent from the same lattice logic; incompatibilities are recontextualized at the substrate level.
Substrate logic → {Relativity ∧ Quantum}
One mechanism, two regimes.
Ghost-Field Degrees of Freedom
Non-massive, non-energetic carriers of pattern resonance (Φghost) influence stability without energy exchange.
Φghost ⊂ Pattern Field
Structure without mass.
Law of Reciprocal Observance
Any observable pattern is, by interaction, also an observer; observation is a field-level reciprocity.
∀P: Observable(P) ⇒ Observant(P)
Allen’s Law (co-observation).
Pattern Field Theory™ - A New Origin Story
PFT reframes “beginning” as Emergence (π-seeded closure and recurrence) followed by the Breach (2D→3D rupture of the stabilized field). Mathematical witnesses- primes, Fibonacci structure, perfect numbers, and π-align with this construction. Empirical echoes across cosmology and pattern imaging are evaluated as tests of AOL-level claims.
Authorship
Pattern Field Theory™ is authored by James Johan Sebastian Allen. Canonical formulations, JSON master archives, and timestamped records (e.g., OpenTimestamps) establish provenance and priority. This site is the authoritative source.
Perfect Numbers and Fractal Closures
Allen Fractal Closure Law (AFCL). In PFT, even perfect numbers appear as binary fractal closure counts on a π-resonant lattice. When p is prime and 2^p − 1 is a Mersenne prime, the corresponding even perfect number is 2p−1(2p − 1). AFCL models this as the total pairwise links among 2p nodes arranged on nested rings (Differentiat™ geometry), expressing how resonance closures accumulate across scales.
For larger p, the pattern extends (e.g., 496 for p = 5), linking AFCL to structures noted in physics and biology. AFCL supplies a consistent counting geometry explaining why perfect-number milestones recur during early 2D lattice stabilization.
Pi-Matrix captured across scales
Archival atomic images and Planck 2018 PR3 CMB products exhibit recurring lattice motifs consistent with AOL-level resonance. See the overview and quantitative spectra workups.
Atoms → Cosmos (overview) Spectra analysis (methods & plots)
Core Principles
- Fractal Reset. Recursive resets preserve coherence while enabling growth and re-synchronization.
- Container Law of Measurement. Measurements are interior to their container; a universe has no external ruler, so absolute size is undefined.
- Dominion Principle. Environments (air, water, vacuum, gravity) define permitted coherences; light illuminates inside gravity-sustained dominions.
- π as Structural Closure. π functions as the first stable closure enabling persistence, memory, and recurrence on the lattice.
- Metacontinuum. The pre-geometric substrate that allows breaches into universe-level domains while remaining outside their measurement frame.
Related research
- 3n+1 growth model. Orbital doubling and closure rules generate structural limits.
- Riemann Hypothesis. Lattice resonance vs. zeta zeros (statistical correspondence studies).
Explore detailed methodologies in Predictions.