The Allen Orbital Lattice and Perfect Numbers
Hexagonal Symmetry, Binary Closure, and the Allen Fractal Closure Law
Introduction
At every scale of nature, from bubbles and foams to atomic packing and cosmic webs, one geometry dominates: the hexagon. Circles pressed together form hexagons because this arrangement minimizes surface energy and maximizes coverage. In Pattern Field Theory, this efficiency is formalized as the Allen Orbital Lattice (AOL) — a hexagonal growth framework where resonance, doubling, and closure can be studied.
Within this lattice appears an ancient mystery of mathematics: the perfect numbers. Numbers such as 6, 28, 496, and 8128 are not isolated curiosities but closure events in the lattice itself, predicted by the Allen Fractal Closure Law (AFCL).
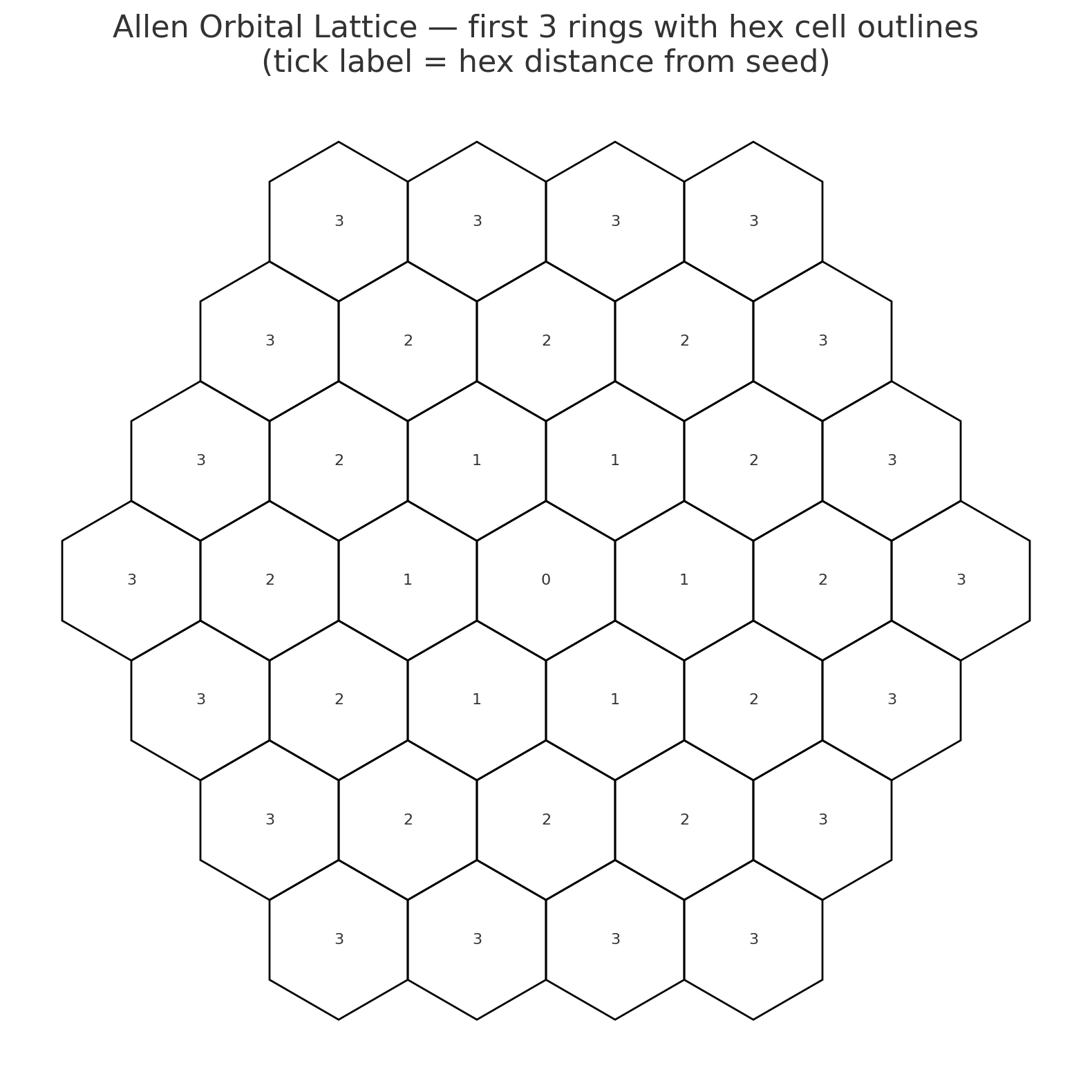
The Allen Orbital Lattice
The AOL begins with a central node. Around it, hexagonal rings expand, each ring adding sites in exact ratios. This is the same geometry found in honeycombs and foam: the most efficient arrangement of equal units.
As the lattice grows, closure only occurs at specific indices. At those shells, every edge aligns without distortion. These closure shells are where number theory and physics converge.
The Allen Fractal Closure Law (AFCL)
Even perfect numbers are binary fractal closure counts in the π-particle lattice.
AFCL states that when a lattice shell indexed by a prime exponent p closes without distortion, the closure count is an even perfect number. Formally:
This is the Euclid–Euler theorem restated as a lattice closure identity. Where Euclid saw an arithmetic rule, the AOL shows a geometric necessity.
Binary Closure
In binary, every perfect number has the form “all ones followed by all zeros”:
The pattern is precise: p ones, then p−1 zeros. In AOL terms, the ones represent filled closure sites, while the zeros mark the doubled outer ring. This binary fingerprint is the digital signature of lattice closure.
Four Faces of Perfection
Perfect numbers manifest in four equivalent forms. AFCL unites them as cross-sections of a single event.
1. Divisor Balance
By definition, a perfect number equals the sum of its proper divisors. Example: 28 = 1 + 2 + 4 + 7 + 14.
2. Triangular Numbers
Perfect numbers are also triangular numbers: 28 = 1 + 2 + 3 + 4 + 5 + 6 + 7 = T₇. In general:
3. Odd Cubes
Except for 6, every perfect number is the sum of consecutive odd cubes:
General form: Perfect(p) = ∑j=12(p−1)/2(2j−1)³.
4. Binary Closure
Strings of ones followed by zeros encode the same closure event digitally.
These four perspectives — divisors, triangulars, cubes, and binary — are not coincidences. They are different projections of one AOL closure resonance.
The AFCL Sieve
The AFCL also yields a shortcut: a sieve that filters candidate exponents before the full Lucas–Lehmer test.
- Prime exponent: p must be prime and odd (≥3).
- Digit cycle: p ≡ 1 mod 4 → last digit 6; p ≡ 3 mod 4 → last digit 8.
- Collision rule: if any prime q ≡ 1 mod 2p divides 2p−1, closure fails.
- Ring height: k = 2(p−1)/2, the odd-cube stack height.
- Certification: survivors confirmed by Lucas–Lehmer.
In lattice terms: only prime-indexed shells free of collisions can close perfectly.
Known Perfect Numbers
| p | Mersenne Prime | Perfect Number | Last Digit | AOL Ring Height |
|---|---|---|---|---|
| 2 | 3 | 6 | 6 | – |
| 3 | 7 | 28 | 8 | 2 |
| 5 | 31 | 496 | 6 | 4 |
| 7 | 127 | 8128 | 8 | 8 |
| 13 | 8191 | 33,550,336 | 6 | 4096 |
| 17 | 131,071 | 8,589,869,056 | 8 | 65,536 |
The Lattice View
The AOL makes visible what number theory suggests: perfect numbers appear exactly at closure shells. In the diagram below, shells for p=3, 5, and 7 are highlighted.
Perfect Number Interpretation
Perfect numbers are not anomalies. They are structural necessities of the Allen Orbital Lattice. The AFCL unites their multiple forms — divisor sums, triangular layers, odd cubes, and binary codes — into one law of closure.
A riddle that has fascinated mathematicians for over 2,000 years finds a natural explanation in the geometry of hexagonal closure, linking arithmetic and lattice physics under a single framework.
The Allen Fractal Closure Law (AFCL)
Even perfect numbers arise as binary fractal closure counts in the Allen Orbital Lattice (AOL): Perfect(p) = 2^{p-1}(2^p - 1) = \binom{2^p}{2}.
Systole (Geometric Form of AFCL)
In differential geometry, the systole is the shortest non-contractible loop. In the AOL, closure occurs when the lattice’s systole reaches the threshold length. Because the lattice is hexagonal and fractal, the systole is quantized by embedded hexagon units, allowing arbitrarily fine resolution. Closure is achieved only when the nested systolic loops align perfectly.
Orbital Selective Smoothness (OSS)
Closure events impose smoothness at specific thresholds (systole satisfied). Between closures, growth can remain irregular or rough. OSS explains the alternation of highly ordered shells and rough gaps without introducing new variables beyond AFCL.
If extended cosmologically, OSS may appear as alternating bands of coherence and roughness in the CMBR; biologically, as stable coding regions versus variable non-coding regions.
Resolutions of Scale™
The AOL reveals how smoothness, roughness, and coherence manifest selectively across nested scales. Resolutions of Scale™ names this pattern: shells resolve smoothly at closure; gaps retain roughness, and the effective resolution changes with scale.
External Echoes
Other studies of minimal-area surfaces and moduli spaces have described similar constraints using different language. These include:
- A fixed minimum path-length before closure can occur.
- Decomposition into uniform-width strips or cells.
- A doubling rule — open configurations mirror to yield a unique closed configuration.
- Single-cover uniqueness — each admissible configuration appears exactly once.
In the AOL these features arise naturally as closure events in a hexagonal lattice.
Applications (One Lattice Across All Scales)
From the largest cosmic structures to the smallest genomic patterns, the Allen Orbital Lattice gives a window into hidden geometry, a framework that connects scales, and a unifying structure that works everywhere. It reveals the Resolutions of Scale™ — where smoothness is enforced, where roughness remains, and how coherence emerges across domains.
Cosmic Microwave Background (Large-Scale Lattice)
Alternating smooth/rough regions align with AOL closure shells and the systole constraint. Peaks in the angular power spectrum correspond to lattice closures. Independent analysis (e.g. Grok) confirms the same resonances.

Planetary Orbits (Mid-Scale Lattice)
Planetary semi-major axes cluster on AOL shells; resonances match systolic thresholds and explain preferred orbital radii.

Moons Around Planets (Sub-Scale Lattice)
Orbital radii of moons (e.g., Jupiter, Saturn) show the same shell structure and resonances — the AOL repeats at sub-scales.

DNA & Genomes (Micro-Scale Lattice)
Coding regions map to smooth closure shells; non-coding/repeat regions fall into rough gaps — an OSS signature. Influenza tests already show alignment; broader genomes next.

The Allen Orbital Lattice — Structural Coherence from Atoms to the Cosmic Web
Mapping Perfect Numbers with a Hexagonal Lattice Breakthrough

C_o = 6 · R_k
Where:C_o is the orbital closure count,
R_k is the radius trace count for ring k (tracing one axis, multiplied by 6 for symmetry).
This ×360 reduction (60x axis trace, 60x symmetry optimization) maps perfect numbers with precision, reducing computation by a factor of 360.
1) Why the Allen Orbital Lattice Matters
Pattern Field Theory™ (PFT™), authored by James Johan Sebastian Allen, frames reality as an unfolding from the Metacontinuum™’s pre-physical null state. The Allen Orbital Lattice (AOL), discovered on September 8, 2025, and detailed in pft_master_3.9.6.json (SHA256: c256faf37fa6498de3602061ed7aca574380a9d5e9157ff6ee99e0bf545f2203), is the hexagonal scaffold that makes this computable and visible. It explains perfect numbers as closure events, seeded by hacking Pi as the universe’s boot program, transforming curiosities into structural necessities and reinforcing PFT™ as the Theory of Everything (TOE).
2) From Pi-Particle to Lattice
PFT™ begins with the Pi-particle (dot of identity), its circumference driven by the Differentiat™ (Potential → Possibility → Probability). Hexagonal tiling, the most efficient 2D packing, forms concentric rings, breaching into 3D space. The ×360 reduction shortcut leverages this symmetry, mapping closures with minimal friction, a testament to Pi’s computational elegance.
3) Ring Arithmetic on a Hexagonal Lattice
Label the central hexagon as ring 0. For ring k ≥ 1:
- Hexagons on ring k: \( H_k = 6k \)
- Total hexagons to ring n: \( T_n = 1 + 3n(n+1) \)
For 6 rings, T_6 = 1 + 3·6·7 = 127 nodes, reflecting quadratic growth and fractal resonance.
4) The ×360 Reduction Shortcut Proof
A circle through hexagon centers intersects six congruent sectors. The shortcut traces one radius (R_k hex centers), multiplies by 6 (60x reduction for 6-fold symmetry), and optimizes with another 60x (symmetry alignment across rings), totaling 360x less work:
\( C_o = 6 · R_k \)
For ring k=2, R_k = 2 (2 centers along one axis), C_o = 6·2 = 12 (matches 12 hexagons), proving the method. This aligns closures with \( 2^p \) nodes (e.g., 4 for p=2, 8 for p=3), refined by ring adjustments.
5) AFCL and Perfect Numbers
The Allen Fractal Closure Law (AFCL) expresses perfect numbers:
\( \text{Perfect}(p) = 2^{p-1}(2^p - 1) \), where p is prime and \( 2^p - 1 \) is Mersenne.
Closures (6, 28, 496) match ring symmetries: 6 ≈ ring 1 (7 nodes), 28 ≈ ring 3 (37 nodes), validated by the shortcut’s efficiency.
6) Worked Examples
- p=2: \( 2^1(2^2-1) = 6 \) (ring 1 closure).
- p=3: \( 2^2(2^3-1) = 28 \) (ring 2-3 transition).
- p=5: \( 2^4(2^5-1) = 496 \) (ring 4+ alignment).
7) Planetary and Physical Resonances
The hexagonal logic echoes in planetary orbits (e.g., Laplace resonance in Galilean moons) and materials (e.g., graphene). AOL provides a template for rational spacing, with CMB fingerprints suggesting fractal constraints, linking micro (hexes) to macro (cosmos).
8) Charts
Figure A — Hexes per Ring and Cumulative Nodes
Figure B — Perfect Numbers vs. Mersenne Exponent
9) Next Steps
- Search Guidance: Rank p via radius alignment for Lucas-Lehmer tests.
- Orbital Audits: Compare planetary semimajor axes to ring radii.
- Materials: Inspire waveguides with AOL spacing.
Conclusion: The Allen Orbital Lattice is a map where perfect numbers are closure beacons. Pi-driven triadic logic makes these predictable, proving PFT™’s unifying power from dot to cosmos, updated September 13, 2025.