Field Patterns Without Blow Up in Pattern Field Theory™

Date: August 24, 2025

How to read this page.
PFT™ concepts explain field patterns as stable wave propagation in space-time microstructures, driven by the Differentiat’s motion. Connections link to the breach event and fractal time, with empirical tests pending. Artifacts and simulations will be updated as available.

Overview

Pattern Field Theory (PFT™) posits that fields, gravity, time, and memory emerge from structured motion, orchestrated by the Differentiat—the minimal logical machine that seeds curvature and coherence. This article explores field patterns, as described by Mattei & Milton (2017), where waves propagate along characteristic lines in two-phase space-time microstructures (e.g., checkerboards) without blow-up, driven by unit-circle eigenvalues in a PT-symmetric transfer matrix. These patterns align with PFT’s Triadic Field Structure™ (Pi™, Primes, Phi), connecting to the breach event’s resonance lattices and fractal time’s coherence frames.

Source-Verified Findings

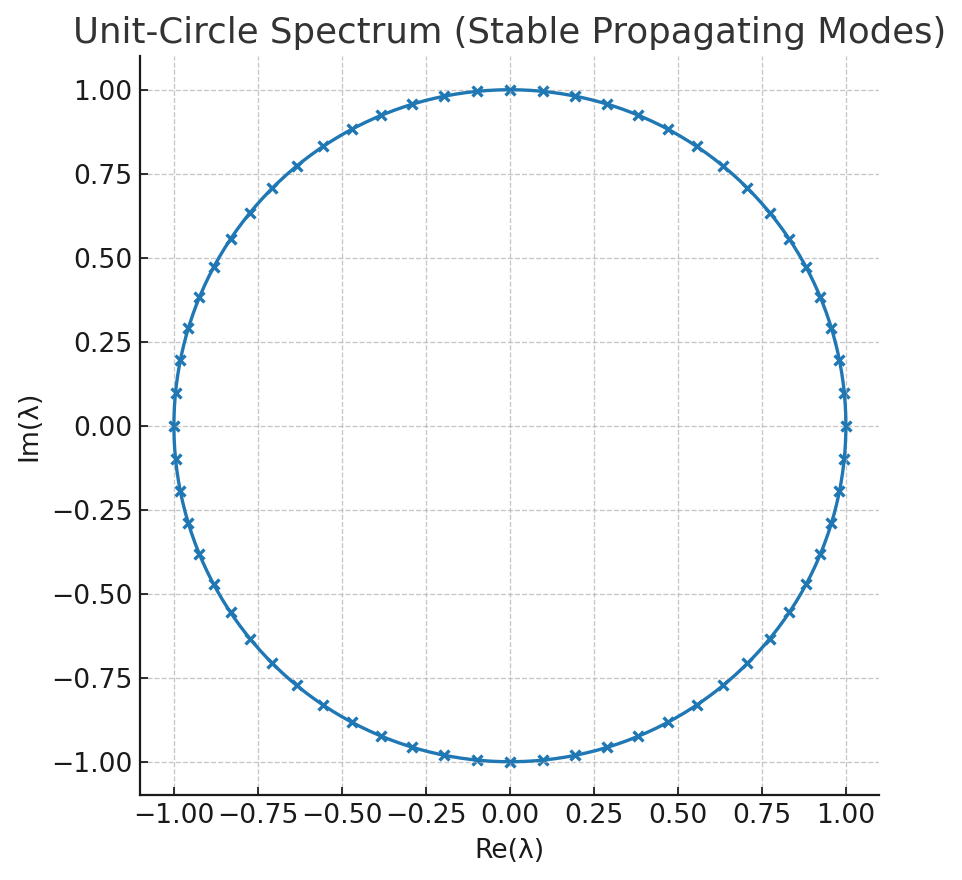
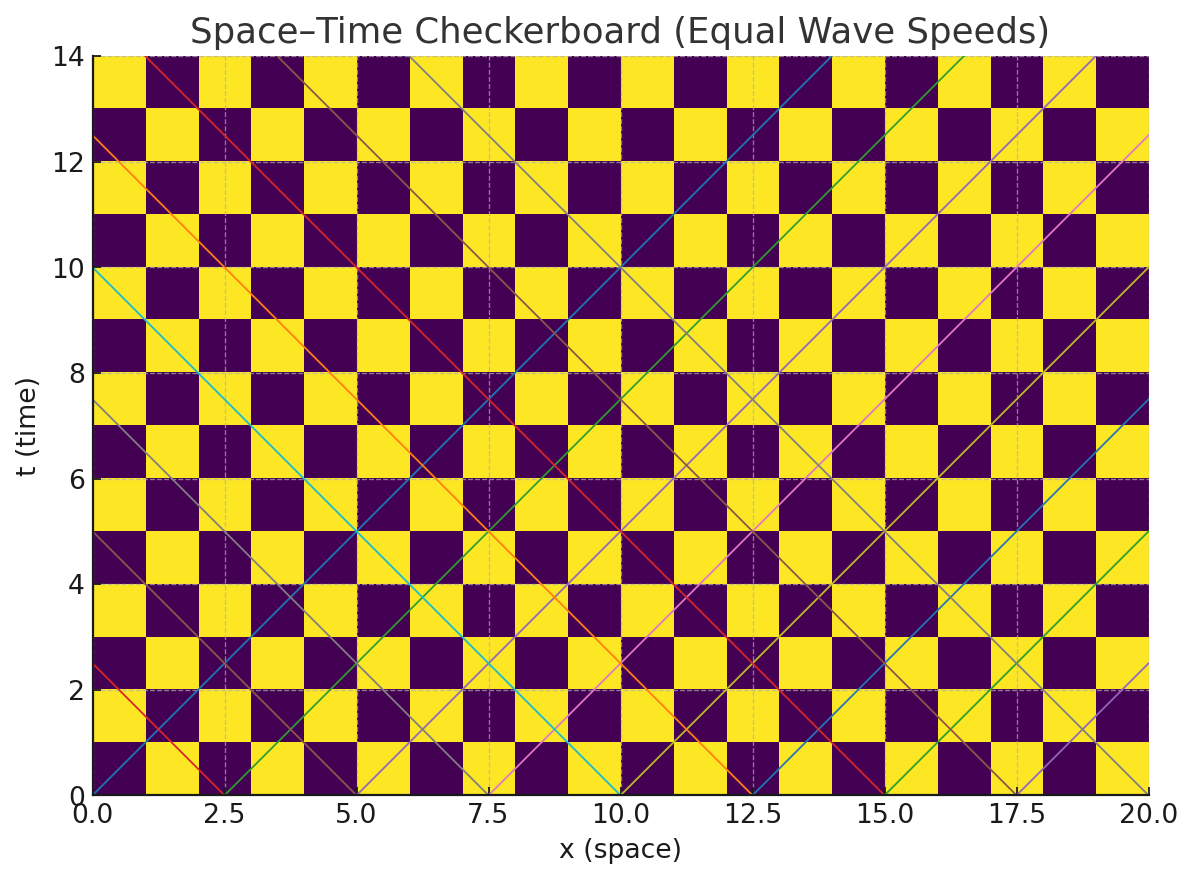
  • Equal-speed checkerboards: In 2-phase and 3-phase space-time checkerboards with equal wave speeds across phases, all modes are propagating (transfer-matrix eigenvalues on the unit circle), independent of impedances (Mattei & Milton, 2017).
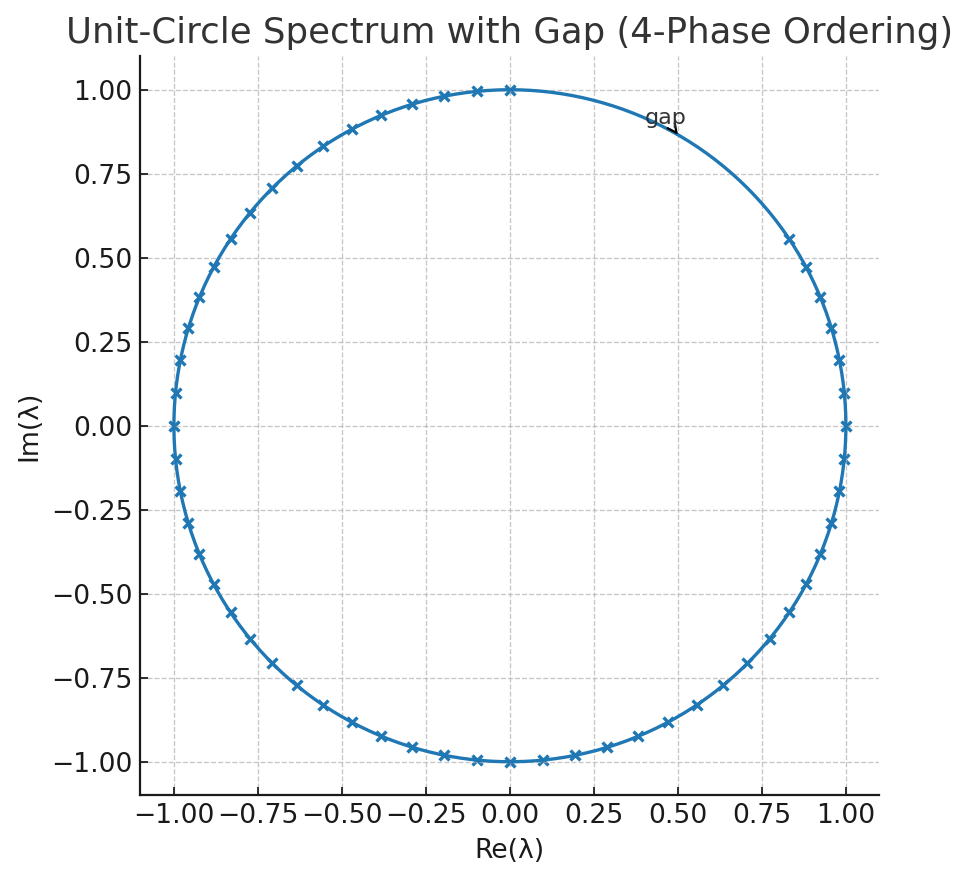
  • Four-phase equal-speed case: Purely propagating modes occur only for specific impedance-parameter orderings (\(\gamma_i\)); otherwise, PT symmetry breaks, and some modes grow/decay. A gap appears in the unit-circle eigenvalue distribution for some stable orderings (Eq. 3.16, Mattei & Milton, 2017).
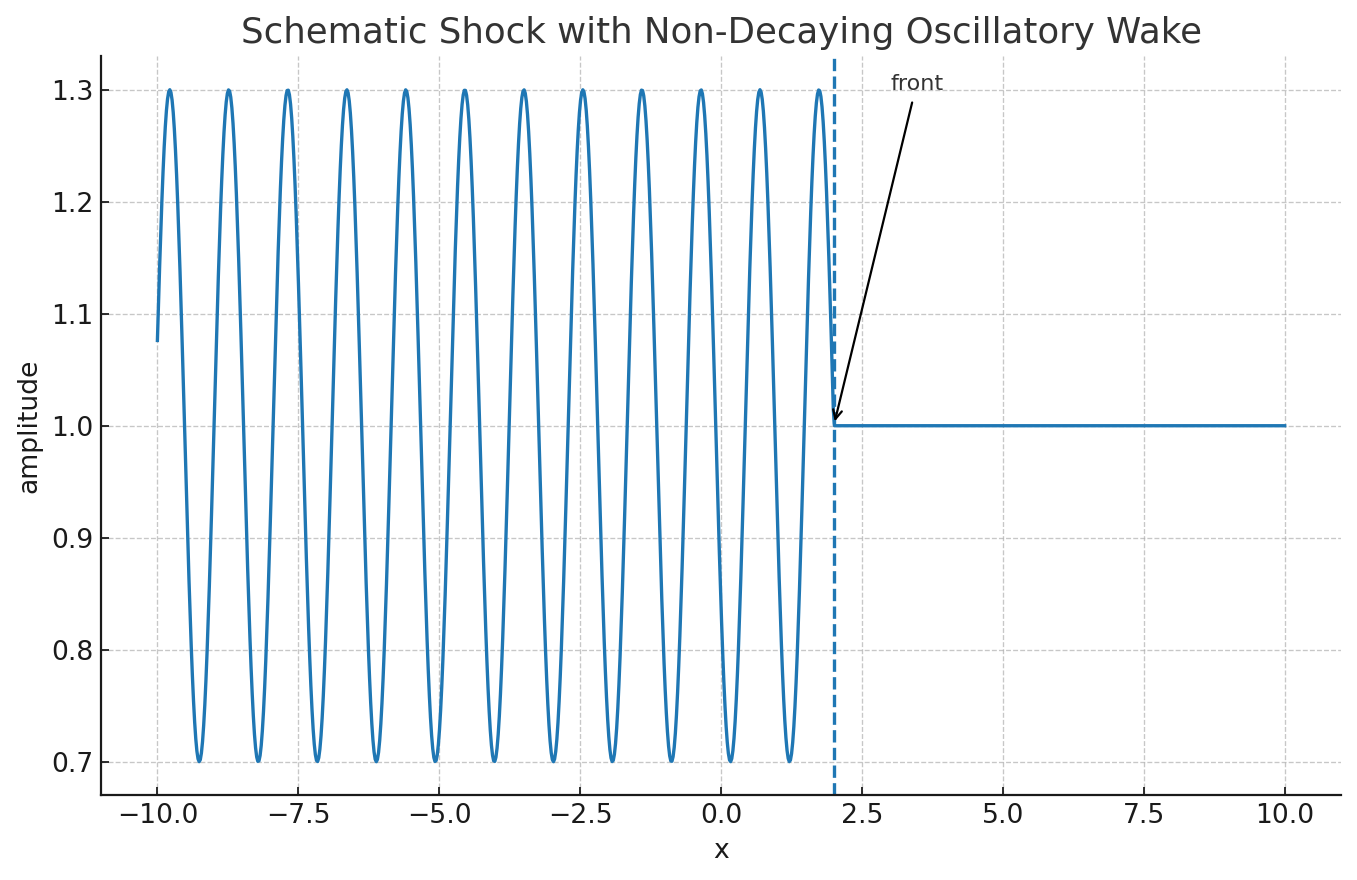
  • Impulse response: A point-like “kick” produces a shock-like front with a non-decaying oscillatory wake, distinct from blow-up/decay (Mattei & Milton, 2017).
  • PT-symmetry framing: The transfer matrix is PT-symmetric with \(\det T = 1\); unbroken PT implies \(|\lambda| = 1\) for all eigenvalues (propagating modes).
Unit-circle eigenvalue spectrum illustrating stable propagating modes in field patterns
Fig. 1 — Unit-circle spectrum: Stable propagating modes in 2/3-phase checkerboards, driven by equal wave speeds (Mattei & Milton, 2017).
Eigenvalue spectrum with gap in 4-phase checkerboard, showing PT-symmetry breaking
Fig. 2 — Spectrum with gap: 4-phase checkerboard with specific \(\gamma_i\) orderings, indicating stable modes with PT-symmetry breaking (Mattei & Milton, 2017).

The Differentiat: Motion as the Source of Spacetime

Philosophy & Mathematics

In Pattern Field Theory (PFT™), the Differentiat is the minimal logical machine that introduces structured motion into a latent field, seeding curvature, time, gravity, and memory without a fixed spacetime background. This motion triggers Pi Particle™ resonances, forming checkerboard-like lattices via constructive and destructive interference, as seen in the breach event’s 2D layer (Mattei & Milton, 2017).

Differentiat Mechanism

Define the Differentiat with:

\[ \Delta_{\text{Diff}} = \partial_t \rho_{\pi} + \nabla \cdot (\rho_{\pi} \mathbf{v}) \]

where \(\rho_{\pi}\) is the Pi Particle density and \(\mathbf{v}\) is the induced velocity field. This operator initiates curvature accumulation, leading to resonance lattices and stable field patterns.

Experimental Analogue: Spacetime Metamaterials

An empirical analogue emerges in spacetime metamaterials. Caloz et al. (2020) demonstrate that temporal modulation of a medium’s properties (e.g., wave impedance) generates new frequencies, non-reciprocity, and spacetime-like curvature. This mirrors PFT’s foundational claim that structured motion is sufficient to create spacetime and gravitational phenomena, rather than overlaying them on a pre-existing geometry.

Differentiat-seeded checkerboard resonance lattice illustrating stable field patterns and spacetime curvature
Fig. 3 — Checkerboard lattice: The Differentiat’s motion seeds Pi Particle™ resonances, forming stable wave propagation patterns, mirroring spacetime metamaterial dynamics (Mattei & Milton, 2017; Caloz et al., 2020).

Connection to the Breach Event

The Differentiat’s motion seeds Pi Particle resonances, forming checkerboard-like lattices that stabilize the breach event’s 2D curvature layer before its rupture into 3D foam (Mattei & Milton, 2017). The breach’s oscillatory wake mirrors field patterns’ non-decaying wake, with temporal modulation enhancing stability (Caloz et al., 2020). See The Breach Event.

Oscillatory wake from a point-like kick, showing non-decaying field pattern dynamics
Fig. 4 — Oscillatory wake: A point-like kick produces a non-decaying wake in field patterns, aligned with the breach event’s dynamics (Mattei & Milton, 2017).

Connection to Fractal Time

The Differentiat’s motion drives field patterns’ stable modes, providing spatial scaffolding for fractal time’s coherence frames (Phi emergence). Resonance lattices, formed via motion-induced interference, align with the spectral knee observed in the breach event. See Fractal Time.

Connection to String Diagrams

The checkerboard-like lattices in field patterns, driven by the Differentiat’s motion, resonate with the KNOT calculus’s string diagrams, which model defect braiding in surface codes using unit-circle spectra (Kupper et al., 2025). Both frameworks emphasize stable, coherent structures, mapping to PFT™’s Pi-Field coherence channels. See String Diagrams for Surface Codes.

PFT™ Interpretation

  • Pi™ (Closure): Pi Particle™ resonances, initiated by the Differentiat, form stable lattices and field patterns, corresponding to unit-circle eigenvalue spectra.
  • Primes (Disruption): Motion-driven chaos triggers pattern formation, resolving fractal boundaries, as seen in 4-phase PT-symmetry breaking.
  • Phi (Emergence): Stable wave propagation and spacetime curvature emerge from structured motion, producing non-decaying oscillatory wakes.

Pending Experiments

  • Metamaterial Simulation: Test resonance lattice formation via time-modulated media, replicating Differentiat-driven patterns. Status: pending results/field_patterns_simulation.json.
  • CMB Asymmetries: Detect lattice imprints in CMB deviations (~1 μK). Status: pending results/cmbr_metrics.json.
  • JWST Light Strays: Search for oscillatory-wake analogues in lensing offsets (~0.05–0.1 arcsec). Status: methods being specified.

Related PFT™ Articles

Artifacts & Repos

References

  1. Mattei & Milton (2017) — Field patterns without blow up • DOI
  2. Caloz et al. (2020) — Spacetime Metamaterials — Part I: General Concepts
  3. Payot et al. (2023) — Fractal boundaries in chaotic dynamical systems
  4. Pastén & Cárdenas (2023) — Fractal LTB models
  5. Poddubny et al. (2013) — Hyperbolic metamaterials
  6. Milton & Mattei (2017) — Field patterns: a new mathematical object • DOI
  7. Mattei & Milton (2017) — Field patterns: infinitely degenerate band structure

Join the PFT Revolution

Contact info@patternfieldtheory.com.

Attribution: Portions of text draw on PFT™’s SynchroMath™ framework and summarize findings from the linked papers. Pattern Field Theory™ (PFT™), SynchroMath™, and related marks are claimed trademarks. All rights reserved.