Rendering and Projection in Pattern Field Theory

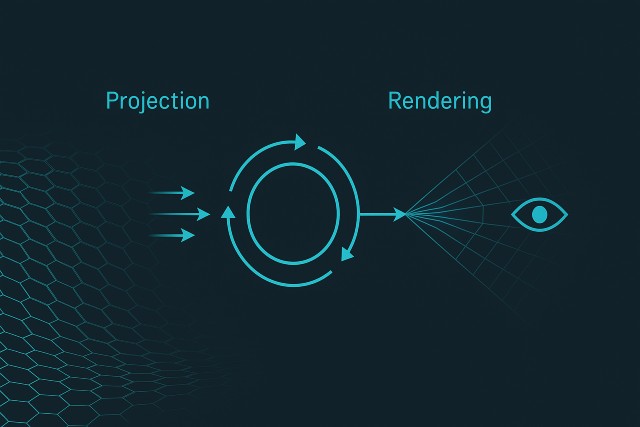
Pattern Field Theory (PFT) defines rendering and projection as complementary processes in the Logical Layer, driving the emergence of conscious awareness from a 2D neural “ghost” layer. This article outlines their interaction, minimal equations, and significance.

Rendering vs. Projection

  • Projection: 2D logical-field patterns (e.g., Pi-Particles, Euler-phase structures) replicate into higher-dimensional frameworks via tension/curvature dynamics on the Allen Orbital Lattice.
  • Rendering: the observer’s anchoring process that stabilizes projected patterns into coherent, observable experiences (selection + consolidation).
  • Complementarity: projection creates potential structures; rendering selects and stabilizes them into reality. Together, they form a recursive feedback loop.

Minimal Mathematical Framework

Projection

Projected pattern field
\[ \Phi_{p}(x,t)\;=\;\sum_{n} \big(P_{n}\,T_{n}\big)\;e^{\,i(\kappa_{n}\,\tau)} \, . \]

Rendering

Rendering (anchoring) operator acting on projected patterns
\[ \Phi_{r}(x,t)\;=\;\hat{\mathcal{A}}(\psi,\,P)\;\Phi_{p}(x,t) \, . \]

Conscious Awareness

Awareness as integrated rendered resonance
\[ \Psi_{c}(t)\;=\;\int \Phi_{r}(x,t)\;R_{E}(x,t)\;dt \, . \]

Symbols: \(P_n\) (pattern weights), \(T_n\) (tension/curvature terms), \(\kappa_n\) (phase curvature), \(\tau\) (proper phase time), \(\hat{\mathcal{A}}(\psi,P)\) (observer-anchoring operator conditioned on state \(\psi\) and priors \(P\)), \(R_E\) (Euler-resonance/entrainment kernel).

Role in Conscious Awareness

Projection generates potential patterns in the logical field; rendering stabilizes them into experienced thoughts, perceptions, and memories. The recursive interplay—enhanced by fractal resonance across scales (self-similar amplification on the AOL)—produces conscious awareness as a dynamic field event:

Fractal reinforcement (optional refinement)
\[ \Phi_{r}^{(\mathrm{fr})}(x,t) \;=\;\sum_{s}\lambda_{s}\,\mathcal{F}_{s}\!\left[\Phi_{r}(x,t)\right], \qquad (0<\lambda_{s}\le 1) \]

where \(\mathcal{F}_{s}\) denotes self-similar reinforcement at scale \(s\) and \(\lambda_s\) controls its strength.

Significance in PFT

  • ✅ Observer problem resolved: observation = resonance/anchoring (not collapse by fiat).
  • ✅ Scale unification: fractal coherence links quantum and cosmic regimes.
  • ✅ Non-local signatures: intuition/entanglement modeled as phase-locked rendering across the mesh.
  • ✅ Black holes: interpreted as failed-rendering zones (projection without retrievable anchoring).

Join the Paradigm Shift

Collaboration & proposals: info@patternfieldtheory.com. PFT is protected under international copyright.